what to do to make them stop as little as possible
How to hit a slalom pole to lose the least speed! The racer, looking for the fastest possible track, gets very close to the poles marking the slalom route. One of the attributes of competitive riding is hitting these poles so that only skis and feet cross the gate. The “rest” of the racer goes over the pole, placing it forward or pushing it aside. Each pole strike stops. How much inhibits – let’s try to estimate. We don’t need calculations with too much accuracy. It’s about letting us know what order of magnitude they are and how much they affect the braking of the riders depending on their height and weight. Let’s describe the simplified model shown in Fig. 10.
The impacted pole receives energy of movement and overcoming the resistance of the hinge, receiving it from the skier.
A skier with a certain weight (including clothing and equipment) gets to a standing pole at a speed of 36 km / h, i.e. 10 m / s. The pole stands upright, is regular in thickness and protrudes above the snow for 1.8 m. The skier touches the pole with a piece of clothing (equipment) and gives it its speed at the point of touch, i.e. vs 10 m / s. The pole touch point receives the skier speed. It can be either at the height of the hand (when the skier hits the hand) or at the height of the knee-boot (when the skier hits by the protector or lower). A moment later, the point of impact slides over the pole and no longer transmits its energy. The pole rotates around the point of insertion at a speed at which the point of impact has a linear speed of 10 m / s. For ease of calculation, we assume that the pole is stiff and does not bend as the pictures actually show. We assume that it is a homogeneous rigid body with a pivot point at the base (in a hinge at snow level). This assumption seems legitimate, because we are not looking at the entire mechanics of pole movement, but only an estimation of the amount of energy that the pole can receive from a skier. By touching the pole, the skier not only turns it around it’s position, but also overcomes the resistance of the swivel. This joint must be strong enough to lift the pole back to vertical position after passing the skier, i.e. give it the potential output energy. The amount of this energy is at least the pole’s potential energy, i.e. the product of the pole’s mass, its average height and acceleration due to gravity.
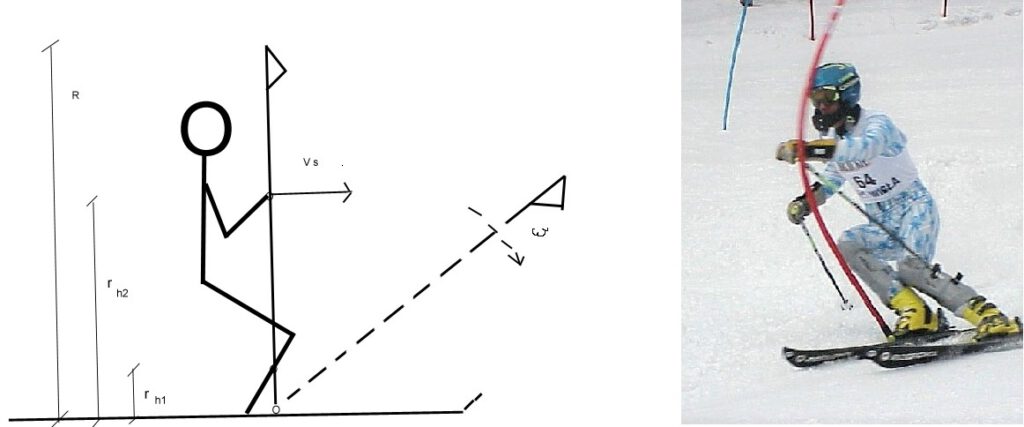
Designations and general assumptions:
Vs – skier speed (let’s assume 10 m / s, i.e. 36 km / h)
Ms – skier mass
Mp – mass of the moving part of the pole (let’s assume 0.4 kg)
Rh1 – the height of the impact with a shoe or protector (let’s assume 0.3 m)
Rh2 – hand hit height (let’s assume 1.2 m)
R – pole height (1.8 m)
ω – angular velocity of the pole lying down
What amounts of energy are transferred:
We calculate the energy of the skier after impact (Eks’) from the general equation for the kinetic energy E = ½ M V2, from which we subtract the kinetic energy of the laying (rigid) pole and the energy stored in the joint. Hence this energy can be expressed as:
Eks ’ = ½ Ms *Vs2 – 1/6 Mp* R2 (Vs / Rh) 2 – Mp* g* R / 2
kinetic energy of the skier kinetic energy of rotated pole energy accumulated in joint
We can also calculate the proportional loss of speed in %.
Calculations on the data for different skiers:
* Child weighing 25 kg has kinetic energy (E = ½ M V2) 1250 J
a) when he hits with his hand Rh = 1.0 [m] loses 25.6 J and 2.05% energy, i.e. 1.01% speed
b) when he hits with a knee-shoe Rh = 0.3 [m] loses 244 J and 19.52% energy, i.e. 10.27% speed

* Junior weighing 40 kg has kinetic energy (E = ½ M V2) 2000 J
a) when he hits with his hand Rh = 1.2 [m] it loses 19 J and 0.95% energy, i.e. 0.46% speed
b) when he hits with a knee-shoe Rh = 0.3 [m] loses 244J and 12.20% of energy, i.e. 6.29% of speed
* 58 kg woman has kinetic energy (E = ½ M V2) 2900 J
a) when he hits with his hand Rh = 1.2 [m] loses (19J) 0.66% energy, i.e. 0.32% speed
b) when he hits with a shoe Rh = 0.3 [m] loses (244J) 8.41% energy, i.e. 4.29% speed
* A man weighing 85 kg has kinetic energy (E = ½ M V2) 4250 J
a) when he hits with his hand Rh = 1.2 [m] loses (19J) 0.45% energy, i.e. 0.22% speed
b) when he hits with a shoe Rh = 0.3 [m] loses (244J) 5.74% energy, i.e. 2.91% speed
Conclusions:
1. Low pole (knee or boot) impact brakes repeatedly (up to 10 times) more than a high-impact pole.
2. Skiers with a lot of weight can sometimes afford to hit the pole lower because their percentage speed loss is rather small.
3. Lighter skiers (women and juniors) should try to hit the poles quite high.
4. Skiers with low weight (children) should not hit the poles at all – they should avoid them, or cover them with an internal hand, so as not to cause impact, but only to bend the pole to the side. In the calculations, the assumed speed was 10 m / s (36 km / h). For children’s riding, a lower speed should be adopted, which would further increase the importance of braking effects.
5. After braking by the striking pole, gravity again accelerates the skier. This acceleration depends on the slope. The skier recovers speed faster on a steep slope and slower on a flat. Hence the conclusion: You can afford a low impact when it is steep, but you should rather not hit on a flat slope.
Hitting a pole always inhibits – let’s minimize this effect!